Why you need Bayesian Optimization
- Imagine yourself in this situation:
- You are supposed to optimize an objective function but you don’t have an explicit mathematical expression of an objective function. As such, you don’t have access to its gradients in order to optimize it with a gradient-based approach
- So maybe you could sample multiple times and use a grid-search approach or even a random search approach to find the optimum value of the objective function. However, each sample is really expensive to get so this approach isn’t really practical
- So what do you really want? You want to sample as little as possible and as intelligent as possible in your quest to find the optimum value of this objective function. Every sample is precious!
- Bayesian Optimization is just what you need!
Bayesian Optimization Algorithm
- Create a probabilistic model of your objective function using a Gaussian Process
- An acquisition function is used to choose which point in the Gaussian Process to sample
- The chosen point is sampled
- The sampled function is used to update the Gaussian Process
- Repeat 2-4 for a specific number of iterations or til the optimal value reaches a satisfiable threshold. You decide!
The Acquisition Function
- The role of the acquisition function is an important one. Probably the most important.
- Its role is to balance exploration and exploitation in a manner that would enable the Bayesian optimization algorithm to reach the optimum value with the least possible number of samples
- Exploration involves sampling states in the Gaussian Process where there is high uncertainty; where the covariance is large. The thinking here is that, if the covariance is large, then the model doesn’t have much information about that state. As such, there’s a possibility that the optimum value could be lurking there. Or not. We don’t know.
- Exploitation involves sampling states with high expected value (mean). Once we’ve found a state with a high value, why don’t we just keep sampling that state? And forget about places in the GP where we are unsure what lurks there. After all, a bird in hand is worth much more than two in the bush.
- But what if there are a gazillion fatter birds with more succulent and juicy meat sitting patiently in the bush, waiting to be kidnapped and cooked for Thanksgiving dinner? Would you risk missing out on all of that?
- The acquisition function, in all its wiliness, figures out a way to do both; to balance exploration with exploitation in such a way to reach the optimum value with a minimal number of samples. There are different flavors of the acquisition function viz;
- Probability of Improvement (PI):
- Only updates its chosen sample if it comes across a state with better value.
- Mathematically expressed as:
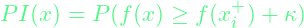
- Expected Improvement(EI)
- Chooses state whose expected improvement from the current state is greatest
- Mathematically expressed as:
![Rendered by QuickLaTeX.com EI(x) = E[f(x) - f(x_i ^+)]](https://alphonsusadubredu.com/wp-content/ql-cache/quicklatex.com-9493e8634334d3d45326cffd18d2fcd6_l3.png)
- Upper Confidence Bound (UCB)
- Simply sums up the mean and the product of the variance and a parameter
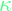 , which is specified based on the user’s preference.
, which is specified based on the user’s preference. - Mathematically expressed as:
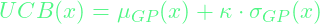
- Simply sums up the mean and the product of the variance and a parameter
- Probability of Improvement (PI):
Example usage of Bayesian Optimization using scikit-optimize Python library
Check out the skopt API documentation in the link provided below for a detailed and documented implementation
https://scikit-optimize.github.io/notebooks/bayesian-optimization.html