03/16/2019
Work by Siddharth Srivastava, Eugene Fang, Lorenzo Riano, Rohan Chitnis, Stuart Russell and Pieter Abbeel
Link to paper: http://people.eecs.berkeley.edu/~pabbeel/papers/2014-ICRA-hierarchical-planning.pdf
They propose a new approach that uses off-the-self task planners and motion planners and makes no assumptions about their implementation. This approach uses a novel representational abstraction and requires only that failures in computing a motion plan for a high-level action be identifiable and expressible in the form of logical predicates at the task level. They evaluate the approach and illustrate its robustness through a number of experiments using OpenRAVE simulator and a PR2 robot.
To perform high-level tasks like cleaning up a kitchen, a robot would have to generate a high-level task plan as well as a low-level motion plan. The task planner generates a routine for performing all the sub-tasks involved in cleaning up the kitchen. An example task plan for this task could be, in this order;
- Move the chairs to their respective positions.
- Empty the left-over food in the dishes into the trash
- Wash the dishes
- Throw out the trash.
A motion planner on the order hand would generate the low-level motor torques and mobile-base velocities required to get the robot to perform all these tasks.
However, combining task planners and motion planners in performing a task isn’t an easy problem because task planners usually do not consider the geometric constraints/preconditions of the physical actions. Even a simple problem like picking up an object, has continuous arguments, preconditions and effects. As a result, the intuitive approach of generating a task plan and doing motion planning on each sub-task often fails.
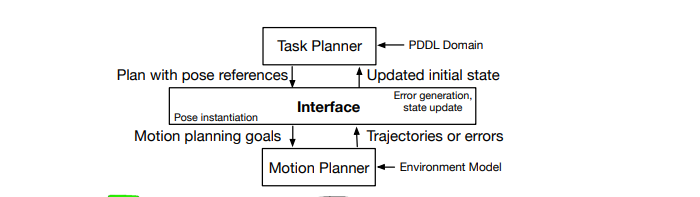
The main contribution of this work is to develop an interface between the task planner and the motion planner that enables the task planner to operate without regard to the geometric constraints of the problem. Physical geometric constraints discovered through reasoning in the continuous space are translated and communicated to the task planner through this interface layer. Figure 1 depicts this configuration
The main ideas of this paper are demonstrated in Figure 2. In FIgure 2, the goal is to move block b1 to table S. A discrete task plan for this problem would describe actions pick and place with the following preconditions and effects: if gripper is empty and pick(b1) is applied, , the gripper holds b1; if the gripper is holding b1 and place(b1,S) is applied, b1 is placed on table S and the gripper no longer holds b1. This description however, is obviously inaccurate since there is a block b2 that obstructs the gripper’s path to b1. To solve this, one might call action pick with pick(b1, traj), where traj represents the obstacle-free trajectory to b1.
This would however not work since Task planning domain descriptions require actions with discrete arguments and thus cannot directly handle this new representation. You could also suggest to discretize traj in order to make it compartible in a Task planner. This would also be wrong and impractical because, even crude discretizations of domains of continuous variables lead to exponential time complexities and computationally impractical problems.
This is where the contribution of this work comes in. This work proposes an approach for communicating relevant geometric information to the Task planner in terms of logical predicates and thus, without discretization.
03/20/2019
To accomplish this, they use symbolic references to continuous values such as ‘grasping pose for box b1’ and ‘trajectory for reaching grasping pose for box b1’. They then use an off-the-shelf planner to generate plans of the form ‘execute pick with a target pose which is a grasping pose for b1 and has a feasible motion plan”. And each of the symbols used in such plans have to be instantiated or refined into numbers. This is, in some cases, not possible because there could be a box b2 that obstructs the path trajectory generated by the plans. This could happen if the geometric preconditions of the task plan weren’t updated. Such a precondition could be in the form of a boolean, which is set to True if there is a clear, unobstructed path in the planned trajectory and False if otherwise. The method proposed in this paper solves this problem by initially initializing the truth values of all relevant preconditions to default values based on the physical conditions of the task and update these preconditions if they change in the course of the task.
Representation
A complete representation of a pick action in PDDL (Planning Domain Definition Language) is as follows;
<strong>pick</strong>(obj, gripper, pose1, pose2, traj)
<strong>precon</strong>: Empty(gripper), At(gripper, pose1),
IsGP(pose2, obj), IsMP(traj, pose1,pose2),
for all obj' not Obstructs(obj', traj, obj)
<strong>effect</strong>: In(obj,gripper), not Empty(gripper),
At(gripper, pose2)
where pick is the pick action , obj is the object of interest, pose1 is the initial pose, pose2 is the goal pose, traj is the motion plan. IsGP(p,o) holds iff p is a pose at which o can be grasped. IsMP(traj, p1,p2) holds iff traj is a motion plan from p1 to p2. Obstructs(obj’, traj, obj) holds iff obj’ is one of the objects obstructing a pickup of obj along traj.
As noted above, continuous variables such as pose1, pose2 and traj are represented as a range over finite sets of symbolic references to continuous values. This representation leads to immense efficiency compared to discretization and makes task planning practical. This approach easily extends to real robots such as the PR2 (see fig. 2).

In the action specification proposed in Figure 2, IsBPFG(pose1, obj), and IsGPFG(pose1, obj), IsBPFPD(pose1, obj, targetLoc) and IsGPFPD(pose2, obj, targetLoc) hold true iff pose 1 is a base pose for grasping or put-down or a gripper pose for grasping or put-down respectively. The predicate IsLFPD(targetLoc, obj) determines whether or not targetLoc is a location where objects can be placed.
The action specifications is illustrated on a simple pick-and-place example in Figure 3.

They then describe two algorithms that constitute the interface layer. Alg. 1 describes the entire Task and Motion Planning algorithm which employs refinement. Alg. 2 describes the refinement subroutine used in Alg. 1.


Pose Generators
The PoseGenerator for an action iterates over those values for pose references which satisfy preconditions of that action. Hence the space of possible values for pose generators can be computed in the pre-processing step in a manner similar to the pre-computation of grasping poses. In their implementation, PoseGenerators iterate over a finite-set of randomly sampled values. Once the MaxTrajCount is reached the sampled values are reset and a fresh random sample is performed. More specifically, a pose generator generates an instantiation of the pose references used in the action’s arguments and a target pose corresponding to each instantiation.
The details of the kinds of pose generators used for pick-up actions and put-down actions can be found in the paper.