Linear Quadratic Regulator (LQR)

alphonsusAugust 21, 2019August 21, 2019Leave a comment

A linear system can be expressed in a linear differential equation as
$\dot{x} = A \cdot x + B \cdot u$
- Where
  - $x$ is the state vector. It contains the values of all the state variables at a particular time
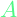  - $A$ is the state-transition matrix. it ‘shows’ how the state changes with time. The product of 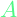$A$ and $x$ gives the state at another time.
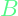  - $B$ is the control or input matrix. Loose definition: Shows the different ways the state can be controlled by $u$ .
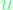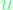  - $u$ is the control vector. It represents the effort applied to the state to transition it into a new state
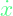  - $\dot{x}$ is the time derivative of the state x.
- For any linear dynamical system, the state-transition matrix, 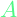$A$ and the control matrix, 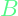$B$ are generally fixed. So in order to drive the system to a specific state, it is the control vector 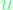$u$ that must be regulated, if the system is controllable; thus, if the rank of the controllability matrix of the system ( $\zeta = [B~ AB~ A^2B~ ... A^{n-1}B]$ ) is n. More on this here
- A common controller for dynamical systems is the proportional controller, expressed as
  $u = -k \cdot x$
  
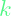  where $k$ is the proportional factor that must be chosen to regulate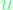 $u$
- Substituting 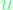$u$ into the state-space representation of the linear system, we end up with the equation
  $\dot{x} = (A - B \cdot k) \cdot x$
- An interesting finding is that, the stability of the system can be determined by the nature of the eigenvalues of the matrix
  - If the real part of any of the eigenvalues of the matrix $[A - B \cdot k]$ is positive, then the system is unstable
  - If the real parts of all the eigenvalues of the matrix $[A - B \cdot k]$ are negative, then the system is stable
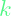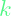- So naturally, since $k$ is the only changeable variable in the matrix $[A - B \cdot k]$ , you’d want to choose a $k$ that makes the eigenvalues of the matrix have negative real parts.
- This can easily be done in Matlab, using the comand
  k = place (A, B, good_eigens)
  
  where good_eigens is a vector of eigenvalues with negative real parts. More on how the place function works in Matlab can be found here
- Choosing the good_eigens vector manually is tricky. This is because, large negative parts of eigenvalues causes instability because the system tends to ‘shoot’ too quickly towards stability, making it overshoot in some cases. Small negative parts of eigenvalues also cause the system to very slowly approach stability. And this might not be ideal in some cases.
- So how to we choose the perfect eigenvalues that lie at the sweet spot between too fast and too slow? Use LQRs!
The LQR algorithm chooses the best eigenvalues by optimizing (minimizing) a cost function whose parameters are specified by the user.
- The cost function, 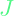is
  $J = \int_{0}^{\infty} (x^T \cdot Q \cdot x + u^T \cdot R \cdot u) \cdot dt$
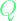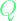  - $Q$ is an nxn matrix that expresses the penalty for the speed at which each of the parameters in the state vector should be reached. 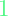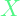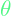For instance: for a state vector $x = \left[\begin{array}{@{}c@{}} X \\ \dot{X} \\ \theta\\ \dot{\theta} \end{array} \right]$ , if it has a $Q$ matrix of $\left[\begin{array}{@{}c@{}} 1~~ 0~~0~~ 0 \\ 0~~4 ~~0~~0 \\ 0~~0~~ 1~~ 0 \\ 0~ ~0~ ~0~~9 \end{array} \right]$ then it means it gives a penalty of $1$ for reaching state parameters $X$ and $\theta$ slowly, a penalty of 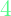$4$ for reaching state parameter 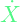$\dot{X}$ slowly and a penalty of 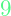$9$ for reaching state parameter 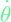$\dot{\theta}$ slowly.
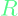  - $R$ is a qxq matrix (where q is the size of control vector 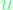$u$ ) that specifies the penalty for using up control effort 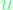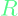$u$ . $R$ would be large if it is expensive to apply control $u$ .
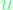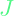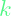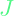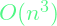- Optimizing the cost function $J$ and solving for $k$ involves solving a Riccati differential equation. Details can be found here. The time complexity for optimizing $J$ is $O(n^3)$ . As such, LQR is intractable for systems with really large state-transition matrices.
- LQR can easily be used to find the optimal 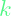$k$ in Matlab by
  k = lqr(A, B, Q, R)
  
  . This 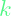$k$ returned gives the matrix $[A - B \cdot k]$ optimal eigenvalues based on the user’s choice of penalty matrices Q and R. More on the lqr Matlab function here.

Leave a Reply Cancel reply